很久没有更新博客了,一直在忙研究生的毕业设计和毕业论文。毕业论文上传盲审之后,每天放松之余花了一点时间阅读这本早就在书立中的《统计数据会说谎》。这本书共分为十章。
1.带有偏差的样本
经典案例:耶鲁大学1924届毕业生平均年收入高达25111美元。
该案例中的样本不具有代表性。25111的平均年收入仅仅能够代表地址明确、愿意公开收入的部分高收入群体。
统计结果受样本影响,抽样方法不合适会导致样本不具有代表性;样本的答案受到其他如政治倾向、个人隐私等因素影响也会导致统计结果不够真实。
随机样本要保证:在一个总体中每个人或每件事被抽到的概率是相等的。当纯随机抽样难度较大时,可以使用分层抽样进行替代。分组比例、每组内部随机样本的抽取都是分层抽样会存在偏差的地方。
任何情况下,统计结果都带有一定的偏差。
2.精挑细选的平均数
案例:XX小区住户平均年收入说法一是15000美元,说法二是3500美元。
平均数究竟是哪一种?——均值、中位数还是众数。
当数据呈现类似“正态分布”的特点,均值、中位数、众数差别不大;然而数据分布呈现倾斜状态时,均值和中位数相差甚远。
3.没有透露的小小数据
案例:使用多克斯牙膏后蛀牙减少了23%。
然而这一广告小字写明仅仅是12个用户参与测试。
只有试验的样本数目足够庞大时,平均数定律才是一个有用的描述或猜测。
观察的结果不代表作者的观点(如金西博士观察发现青少年的性行为是普遍存在的,是正常现象。然而这并不代表他“赞成”这一行为)
没有任何人能在任何方面达到绝对标准,好比抛100次硬币,几乎不可能50次正面50次反面。要搞清楚“正常的”和“理想的”。
在没有重要数据的情况下,不要轻易相信一个平均数、一张图表或者一条趋势线。否则,会盲目地根据平均气温选择露营地点而忽略了温差。
4.无事瞎忙
案例:Peter智商98,Linda智商101,"正常水平"为100。
Linda比较聪明,高于平均水平,Peter就不聪明?
任何测验都有一定的误差:概率误差和标准误差。假如智力测验的误差为3%,Linda的智商就是 ,Peter的智商为。因此,对待智商和其他抽样结果应该看范围 ,要时刻谨记 号。
只有显现出来的差别有意义时才可称之为差别。如香烟的有毒成分差异很小,但最后一名却利用这种排名大肆宣传捞金。
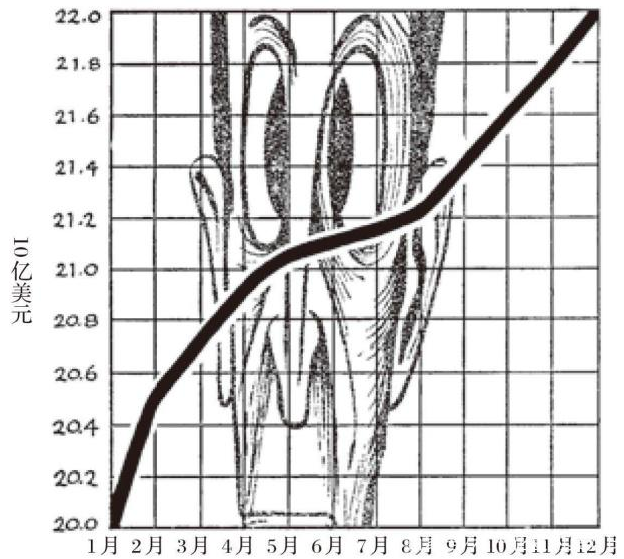
5.惊人的图形
改变图标纵坐标和横坐标的比例、截短图表,可以将变动较小的数据夸张成波动幅度较大的效果。
6.一维图形
使用图画来表明数据时,尤其是数据之间的倍数关系时,使用巧妙的图形可以夸大数据之间的差距。
如一个钱袋表示30美元,再画一个两倍高的钱袋表示60美元,实际上的视觉效果却是4倍(宽、高都是两倍)。如果图像在现实中是立体的,如高炉,甚至视觉上达到了8倍。

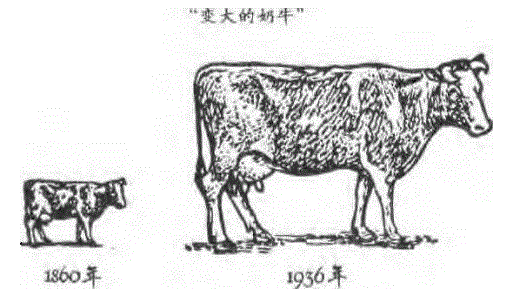
不过随意改动物体尺寸也有弊端。如奶牛数量的增长如果以图形表示,会被误解为奶牛体积的增长。
7.看似相关的数据
如果无法证明自己想要证明的东西,就展示一些其他东西,假装它们是一样的(相关的)。这时人们容易得出错误的结论。
例1:半盎司特效药可以在11秒内杀死试管中31108个细菌。
- 实际上,特效药在试管里效果明显不代表在人体咽喉中也明显,特别是常规服药会对药物进行稀释。
- 也许感冒根本不是细菌引起的
例2:27%的名医抽XX品牌的烟
- 这个数据其实并不代表XX品牌的香烟就更加健康,医生未必比你更加了解香烟。
例3:因为晴天的事故比雾天的事故多,所以雾天开车更安全。
- 实际上,仅仅是因为晴天比雾天多,雾天开车更危险。
例4:现在与过去相比,更多的人死于飞机失事,所以现在的飞机更危险。
- 实际上仅仅是因为现在坐飞机的人是以前的成千上万倍。
例5:1898年战争期间,美国海军的死亡率是0.9%,而纽约市民的死亡率是1.6%,所以待在部队更加安全。
- 实际上,两组数据没有可比性,海军的主要构成人员的年轻力壮的青年人,而市民中包含了婴儿、老年人和病人等。
8.因果颠倒
“如果B事件发生在A事件之后,那么就是A时间引起了B事件”,这是一种非常古老的谬误推理。
为了避免陷入这种谬误,需要严格检验各种与相关性有关的说明。相关性往往通过一些令人信服的精确数据来证明两件事情之间的因果关系,然而相关性却有多种类型:
- 机缘巧合之下得出的相关。样本规模较小时,任何两个事物之间都能建立显著的相关性。例如XX牙膏能减少蛀牙,其实是一次小规模实验偶然的结果。
- “协变关系”,两个变量存在相关性,但无法确定因果。某些情况下会随时交换位置,有时互相既是因又是果。例如收入和拥有的股票。
- 变量之间不存在因果关系,但变量之间的确存在某种相关性。例如抽烟者成绩也不好。此时,两个变量可能都受到第三个因素的影响。
当原本论证的相关数据超出一定范围,正相关达到一个极点就会转变为负相关。雨水越多,庄稼长势越好。然而超过一个极点时,雨水越多,庄稼收成就会减少。
相关表示的是一种趋势,并非人们理想的“一对一”关系。受教育一般能增加收入,但也能证明教育会使某人破产。我们要时刻谨记:即使相关性存在并有真实的因果关系,仍然不能凭此进行决策。
如何避免被一个真实的相关被拿去支持的未经证实的因果关系所迷惑,想想相关发生的过程以及整个时代背景。
案例:XX岛的人认为虱子有益于身体健康,因为健康的人身上都有虱子,而体弱者没有。
- 事实是,体弱者多是因为发烧,而体温升高又导致虱子离开身体。因此是健康不发烧才会有虱子。这里将因果颠倒了。
9.如何操作统计
通过利用统计材料给人传递错误的信息,这一行为在统计学上可称为人为操纵。刻意歪曲、故意操纵统计数据的人不是专业的统计学家,只要这些错误是单方面的,我们就很难将之归咎于粗心或者意外。
例1:基金会统计的美国家庭平均年收入是5004美元,而美国人口普查局统计的同年美国家庭平均年收入却是3100美元。
- 基金会使用了“均值”平均数,而非更小但更为贴切的中位数
- 基金会假设家庭收入与家庭人数成正比,然而事实并非如此。
例2:4.9%的兼职家庭帮工周工资为18美元
- 实际上,这4.9%仅仅是两个人,这一类帮工的总人数也就41人
- 根据小规模样本得出一个具有误导性的百分数
例3:现在购买圣诞礼物可少花100%的钱
- 这并不意味是免费的,省下的钱相当于新价钱的100%,实际上就是打五折了。
- 通过混淆、更换基数,让人产生错觉。
例4:一年365天减去122天睡觉的时间,45天三餐的时间,90天暑假时间,21天法定节假日,最后剩余的时间甚至不够你过周末。
- 将一些不该相加的东西相加在一起就会产生许多愚蠢的错误和强词夺理的狡辩。
- 将各种百分比加在一起纯粹异想天开:买了20样东西,每一样的价格都上涨了5%,加在一起是100%,所以生活成本翻了一番?
例5:投资回报率从第一年的3%上涨到第二年的6%。可以说增加了3个百分点,也可以说增长高达100%。
- 混淆了百分比和百分点,也是极具欺骗性。
例6:在某次数学测验中,比较John与其他同学时使用百分位数。如300人参与,前三名的百分位数就是99,4-6名是98。
- 实际上,百分位数99的学生比百分位数90的学生优秀一点,但是百分位数40和60的学生水平差不多。
- 正态分布的数据中,特征聚集在平均数周围,百分位数具有欺骗性。
例7:去年1夸脱牛奶价格为20美分,一条面包价格为5美分,而今年牛奶价格降至每夸脱10美分,面包价格涨到一条10美分。
- 将去年看作基期,牛奶价格下跌一半(50%),面包价格上涨一番(200%),平均数是125%,所以物价上涨了25%。
- 将今年看作基期,去年牛奶价格是今年两倍(200%),面包价格是今年一半(50%),平均数是125%,所以去年物价比今年高25%,即物价降低了25%。
- 使用几何平均数,将去年作为基期,50%乘以200%,再开方,结果是100%,物价没有变化。
- 基期就是确定开始计算的时间,也就是时间范围内的初值。通过更改基期和平均数计算方式,可以达到欺骗或者迷惑的目的。
统计学是一门科学,也是一门艺术。在允许的范围内,可以进行大量的统计操纵,甚至扭曲事实。一般的统计学家从多个方法中选出一个阐述事实的方法,这是一个主管的过程。然而在商业活动中,统计学家不会选择对自己不利的方法。
10.如何反驳统计数据?
并非所有统计信息都能用设备检验,但是可以提出5个简单的问题来避免被一些似是而非的东西所迷惑。
是谁这么说?
要找到偏差,包括有意识的偏差和无意识的偏差。有意识的偏差如选出对自己有利的数据、改变衡量的标准、使用不恰当的测算方式(中位数更能说明问题时却使用均值,还用“平均数”这种措辞)。
要警惕各种“专家”,确定到底是不是权威人士。
他怎么知道?
样本是否带有偏差,案例是否多到具备显著性?要确保样本的规模足够庞大才能根据这个样本得出真实可信的结论。
漏掉了什么?
当数据来源关系到利益关系时,数据缺乏会让人对整件事产生怀疑。比如一个相关如果缺乏可信的测算方式检验,就未必真相关。
要留心未加说明的平均数。
当没有其他数据作为对比时,数据本身会变得没有意义。
只给出百分数,却没有给出原始数据的材料也往往带有欺骗性。如大学1/3的女生嫁给了大学男老师,然而当年只有3名女生。
如果给出了一个指数,往往要注意是否漏掉了基数。
有时漏掉的还有导致变化的因素。
有人偷换了概念吗?
要注意原始数据和最终结论之间是否存在被偷换概念的地方。如某个候选人在一场非官方的民意测验中获胜并不一定意味着他会在选举中获胜。
这是否合乎清理?
任何以一个未经证实的假设为基础的结论都需要问问“这是否合乎情理”。例如假设词语和句子的长度决定了文章的阅读难度,从而使用公式进行难度判断,这不合情理。
看研究和预测中用到的图表时要谨记:截至目前的趋势或许是事实,但是未来的趋势不过是预测者的猜测。

 支付宝
支付宝  微信
微信