如何用图卷积网络（GCN）在图上做深度学习——翻译自此文

第一部分：对图卷积网络的高层次介绍

图上的机器学习是一项非常困难的任务，因为图是非常复杂但又是信息量丰富的图结构。这篇博客是介绍如何用图卷积网络在图上做深度学习的系列第一篇。GCN是一种非常厉害的神经网络，被设计来直接应用于图并使用图的结构信息。

在这篇博客中，我会对GCNs做个介绍并用代码实例来阐释信息是如何通过隐藏层进行传播的。我们将会明白GCN是如何从前面的层中聚集信息的，并且这种方法是如何产生途中节点的有用的特征表示。

什么是图卷积网络？

GCNs是一种非常有力的用于图上机器学习的神经网络结构。事实上，因为他们太厉害了以至于即使是随机初始化的2层的GCN也能产生网络中的节点的有用的特征表示。下图展示了产生网络中节点2维特征的GCN是如何不经训练保存他们的相对距离。

img

形式上，一个图卷积网络（GCN）是一种对图进行操作的神经网络。给定一个图$ G=(E,V) $ ,一个GCN网络将如下作为输入：

  • 一个输入的维度${N} \times {F}^{0} 的特征矩阵的特征矩阵 X ，其中，，其中， N $ 是节点数量，$ F^{0}$ 是每个节点的输入特征数
  • 一个 $N \times N $ 的图结构矩阵表示，比如邻接矩阵$ A $

一个GCN的隐藏层因此可以记作 $H^i = f(H^{i-1},A) ，其中，其中 H^0 = X $ ，并且ff 是一次传播。每一层$ H^i $ 对应于一个$ N \times F^i $ 的矩阵，矩阵的每一行是一个节点的特征表示。在每一层，这些特征聚集在一起在传播规则 $ f $ 的作用下形成下一层的特征。以此类推，特征在每一个连续的层变得越来越抽象。在这个框架下，各种各样的GCN只是在传播规则 ff 上有区别。

一种简单的传播规则

一种最简单的传播规则就是：$ f(H^i, A) = \sigma(AHiWi) $

其中$ W^i $ 是$ i 层的权重矩阵，层的权重矩阵，\sigma$ 是非线性激活函数（如ReLUReLU 函数。权重矩阵的维度是$ F^i \times F^{i+1} $ ，换句话说，权重矩阵的第个维度的大小决定了下一层的特诊数。如果你对卷积神经网络比较熟悉的话，这个操作和过滤操作非常相似，因为这些权重是被图中的节点所共享的。

简化

让我们的看看传播规则最简单的情况下是如何操作的。令：

  • $ i=1，s.t. f $ 是输入特征矩阵的函数

  • σ\sigma 是恒等函数

  • 选择权重 s.t.AH0W0=AXW0=AXs.t. AH^0W^0=AXW^0=AX.

    换句话说，f(X,A)=AXf(X,A)=AX 。这种传播规则可能太简单了，但是稍后我们会加上丢失的部分。PS:现在 AXAX 等同于多层一个多层感知机的输入层。

一个简单的图实例

作为一个简单的案例，我们使用如下有向图：

img

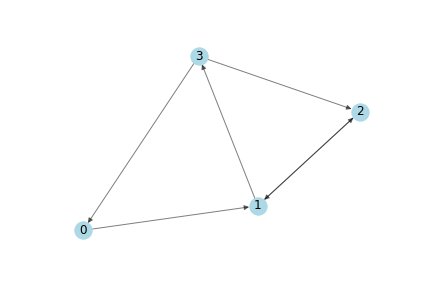
如下是numpy 邻接矩阵表示

A = np.matrix([
    [0, 1, 0, 0],
    [0, 0, 1, 1], 
    [0, 1, 0, 0],
    [1, 0, 1, 0]],
    dtype=float
)

接下来，我们需要特征。我们基于每个的节点的索引（index）产生2个整数特征。这会使得后续的矩阵手动计算较为简单验证。

In [3]: X = np.matrix([
            [i, -i]
            for i in range(A.shape[0])
        ], dtype=float)
        X
Out[3]: matrix([
           [ 0.,  0.],
           [ 1., -1.],
           [ 2., -2.],
           [ 3., -3.]
        ])

应用传播规则

现在，我们有一张图，它的邻接矩阵AA 和输入特征xx 的集合。让我们看看应用传播规则后会发生什么呢？

In [6]: A * X
Out[6]: matrix([
            [ 1., -1.],
            [ 5., -5.],
            [ 1., -1.],
            [ 2., -2.]]

发现了没？每个节点的表示（每一行）现在是它的邻居特征的总和。换句话说，图卷积层用节点的邻居来表征每个节点。我鼓励你们自己验证以下。注意，在这个案例中，节点 nn 是节点 vv 的邻居如果从vv到nn存在一条边。

显而易见的问题！

你也可能发现如下问题：

  • 一个节点的汇集表示不包含自己的特征。一个节点的表征是它邻居节点的特征的汇集，所以只有自循环的节点才会在汇集后包含他们自身的特征
  • 拥有大度数的节点在特征表征中会有较大的值，而度较小的节点特征表征的值也会小。这会导致梯度消失或者梯度爆炸，也是随机梯度下降算法的问题，随机梯度下降算法常被用来训练这种网络并且对每个输入特征的尺度范围较为敏感。

接下来，我分开讨论这两个问题。

加上自循环

为了解决第一个问题，只需给每个节点加上简单的自循环。实际上，只用给邻接矩阵AA在应用传播规则之前加上一个单位矩阵II 。

In [4]: I = np.matrix(np.eye(A.shape[0]))
        I
Out[4]: matrix([
            [1., 0., 0., 0.],
            [0., 1., 0., 0.],
            [0., 0., 1., 0.],
            [0., 0., 0., 1.]
        ])
In [8]: A_hat = A + I
        A_hat * X
Out[8]: matrix([
            [ 1., -1.],
            [ 6., -6.],
            [ 3., -3.],
            [ 5., -5.]])

因为现在节点也是他自己的邻居，在求和邻居节点的特征时也包含了节点本身的特征！

规范化特征表征

通过度矩阵DD的逆D−1D^{-1} 与邻接矩阵相乘，特征表征可以得到规范化。基于此，我们简化的传播规则如下：

$ f(X, A)=D^{-1}AX $

让我们看看会发生什么！我们先要计算度量矩阵。

In [9]: D = np.array(np.sum(A, axis=0))[0]
        D = np.matrix(np.diag(D))
        D
Out[9]: matrix([
            [1., 0., 0., 0.],
            [0., 2., 0., 0.],
            [0., 0., 2., 0.],
            [0., 0., 0., 1.]
        ])

在应用传播规则之前，我们看看邻接矩阵变形前后的变化。

A = np.matrix([
    [0, 1, 0, 0],
    [0, 0, 1, 1], 
    [0, 1, 0, 0],
    [1, 0, 1, 0]],
    dtype=float
)
In [10]: D**-1 * A
Out[10]: matrix([
             [0. , 1. , 0. , 0. ],
             [0. , 0. , 0.5, 0.5],
             [0. , 0.5, 0. , 0. ],
             [1. , 0. , 1. , 0. ]
])

观察可以发现，邻接矩阵每一行的权重已经被对应于这一行的节点的度除法运算了。我们对变形后的邻接矩阵应用传播规则。

In [11]: D**-1 * A * X
Out[11]: matrix([
             [ 1. , -1. ],
             [ 2.5, -2.5],
             [ 0.5, -0.5],
             [ 2. , -2. ]
         ])

得到对应于邻居节点特征的均值的节点表示。这是因为变形后邻接矩阵中的权重对应于邻居节点特征加权和中的权重。还是同样的，鼓励你们自己验证一下结果。

将所有一起看

我们现在将自循环和规范化的方法结合。另外，我们会重新引入我们之前为了简化讨论所忽略的权重和激活函数。

加回权重

第一件要紧事就是加上权重。注意，这里的D_hatD\_hat 是矩阵 A_hat=A+IA\_hat = A+I 的度量矩阵， 即带有自循环的矩阵AA的度量矩阵。

In [45]: W = np.matrix([
             [1, -1],
             [-1, 1]
         ])
         D_hat**-1 * A_hat * X * W
Out[45]: matrix([
            [ 1., -1.],
            [ 4., -4.],
            [ 2., -2.],
            [ 5., -5.]
        ])

如果我们想要减少输出特征表征的维度，我们可以减小权重矩阵WW的尺寸：

In [46]: W = np.matrix([
             [1],
             [-1]
         ])
         D_hat**-1 * A_hat * X * W
Out[46]: matrix([[1.],
        [4.],
        [2.],
        [5.]]
)

加上激活函数

我们选择保留特征表征的维度并且用上ReLUReLU激活函数。

In [51]: W = np.matrix([
             [1, -1],
             [-1, 1]
         ])
         relu(D_hat**-1 * A_hat * X * W)
Out[51]: matrix([[1., 0.],
        [4., 0.],
        [2., 0.],
        [5., 0.]])

瞧！！一个带有邻接矩阵、输入特征、权重和激活函数的完整的隐藏层。

回归现实

现在，最后，我们可以应用图卷积网络在实际的图上。我会展示我们之前看到的如何产生特征表征。

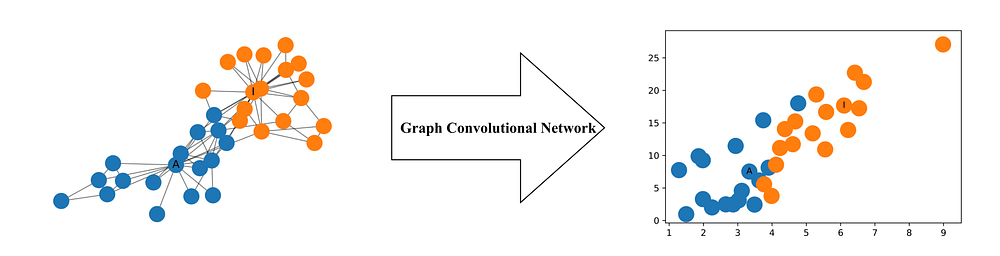
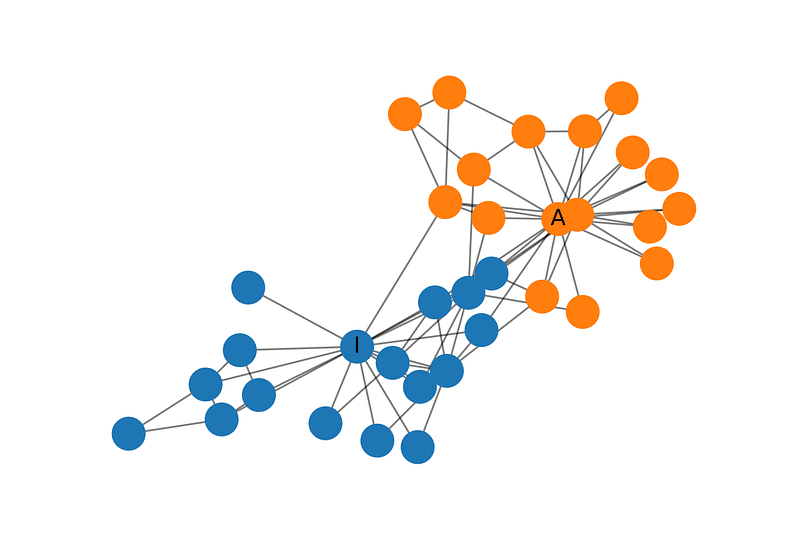
Zachary's Karate Club

Zachary's Karate Club 是广泛使用的社交网络，其中节点表示俱乐部的会员，边表示他们的相对关系。当Zachary在研究这个俱乐部时，一个在管理者和指导者之间的矛盾出现，导致俱乐部一分为二。下图展示网络的图表示，节点根据俱乐部的部分进行的标注。管理员和指导者分别记为AA 和 II 。

img

建立GCN模型

现在，我们来建立图卷积网络。我们不会实际训练这个网络，只是简单随机初始化来产生我们在这篇博客一开始看到的特征表征。我们使用networkxnetworkx ，它使得俱乐部的图表征简单易得，计算A_hatA\_hat 和 D_hatD\_hat 矩阵。

from networkx import to_numpy_matrix
zkc = karate_club_graph()
order = sorted(list(zkc.nodes()))
A = to_numpy_matrix(zkc, nodelist=order)
I = np.eye(zkc.number_of_nodes())
A_hat = A + I
D_hat = np.array(np.sum(A_hat, axis=0))[0]
D_hat = np.matrix(np.diag(D_hat))

我们接下来随机初始化权重。

W_1 = np.random.normal(
    loc=0, scale=1, size=(zkc.number_of_nodes(), 4))
W_2 = np.random.normal(
    loc=0, size=(W_1.shape[1], 2))

叠加GCN层。我们在这里使用单位矩阵作为特征表征，即每个节点用独热编码分类变量表示。

def gcn_layer(A_hat, D_hat, X, W):
    return relu(D_hat**-1 * A_hat * X * W)
H_1 = gcn_layer(A_hat, D_hat, I, W_1)
H_2 = gcn_layer(A_hat, D_hat, H_1, W_2)
output = H_2

我们提取特征表征

feature_representations = {
    node: np.array(output)[node] 
    for node in zkc.nodes()}

最后，瞧！特征表征清晰得俱乐部的团体，即使我们还没有开始训练。

img

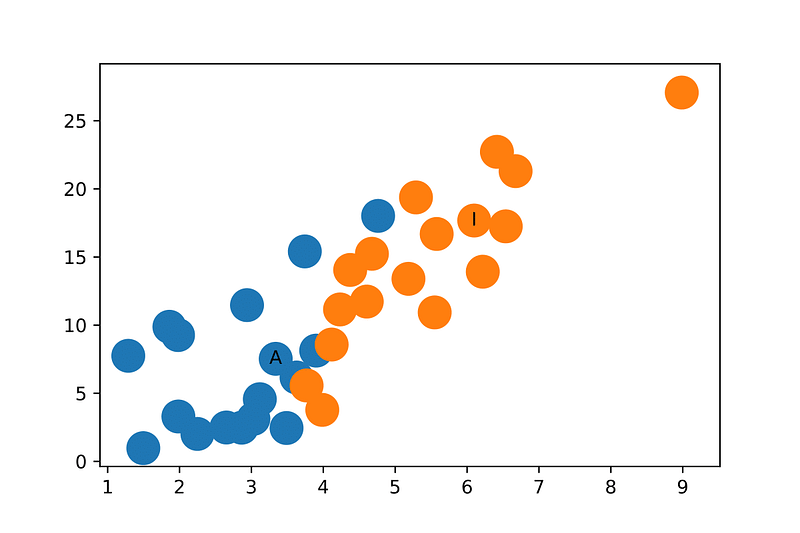
我需要说明的是在这个例子中随机初始化的权重很有可能在ReLUReLU函数后再x轴或者y轴是0，所以多随机几次才能产生上图。

结论

在这篇博客中，我从较高层次对图卷积网络进行了介绍并且阐释GCN每一层的每一个节点的特征表征是如何基于它们邻居的汇集。我们可以看到我们是如何通过numpy来构建网络，他们是如此强大：即使是随机初始化的GCNs也能分开俱乐部的团体。